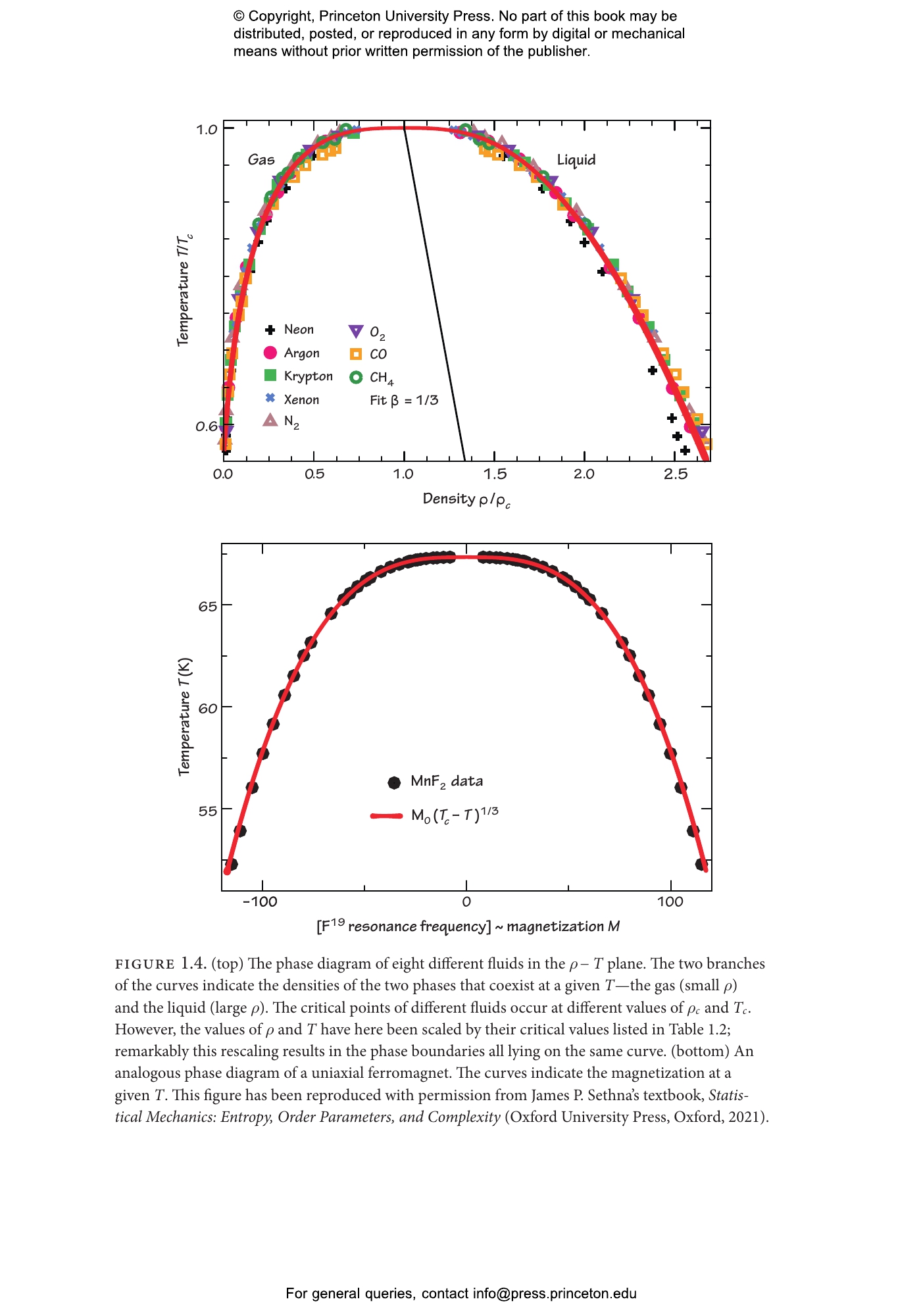
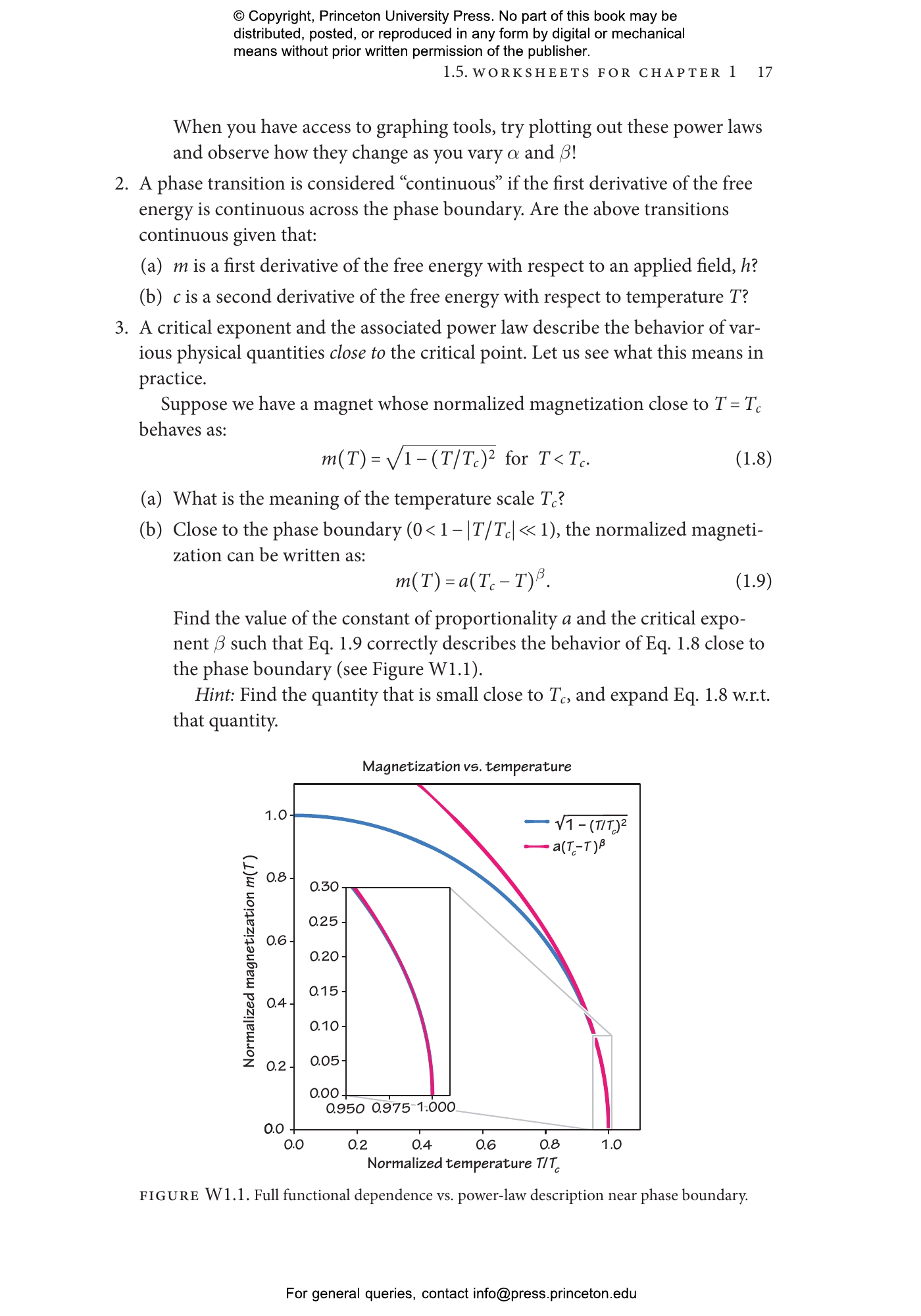
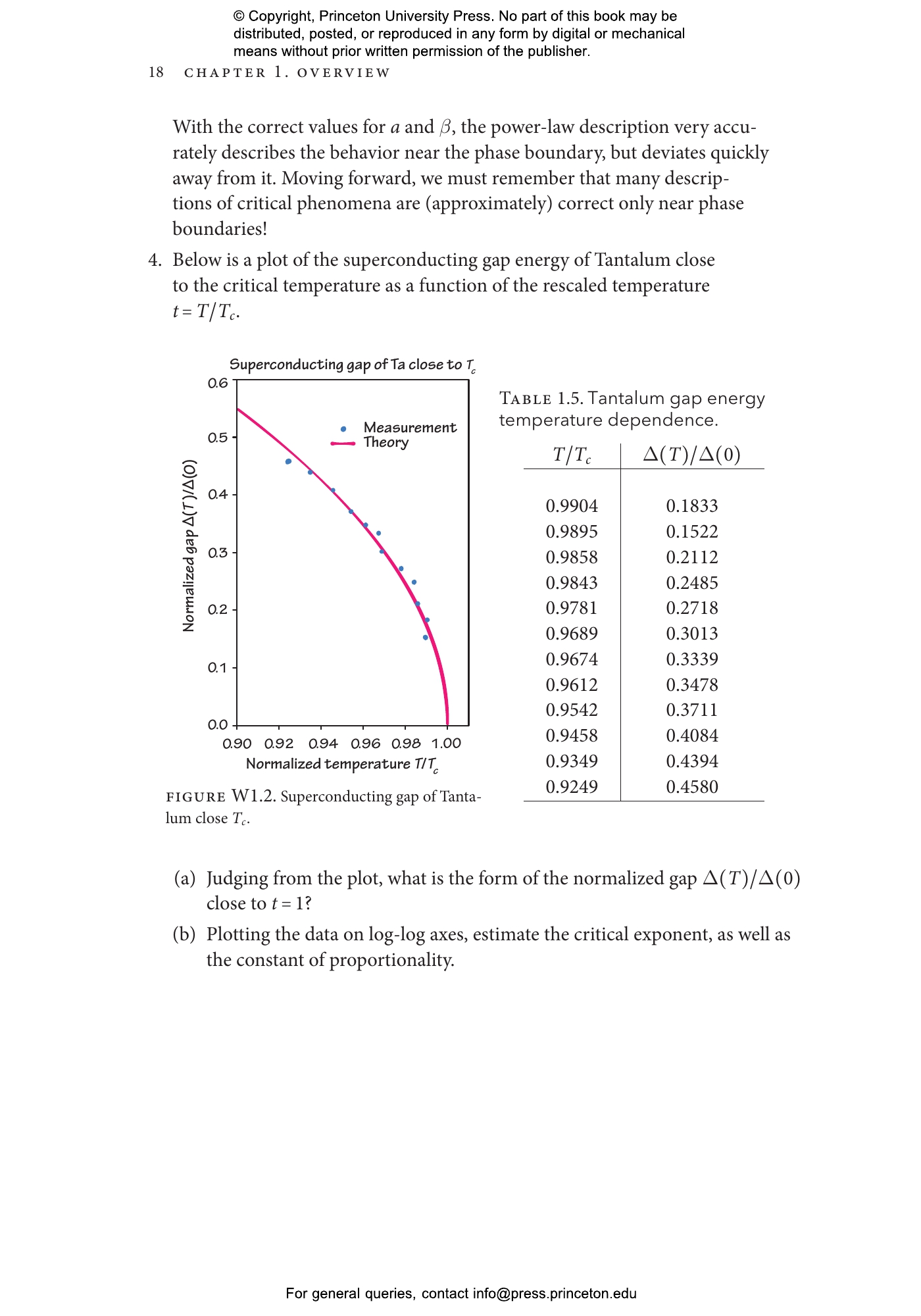
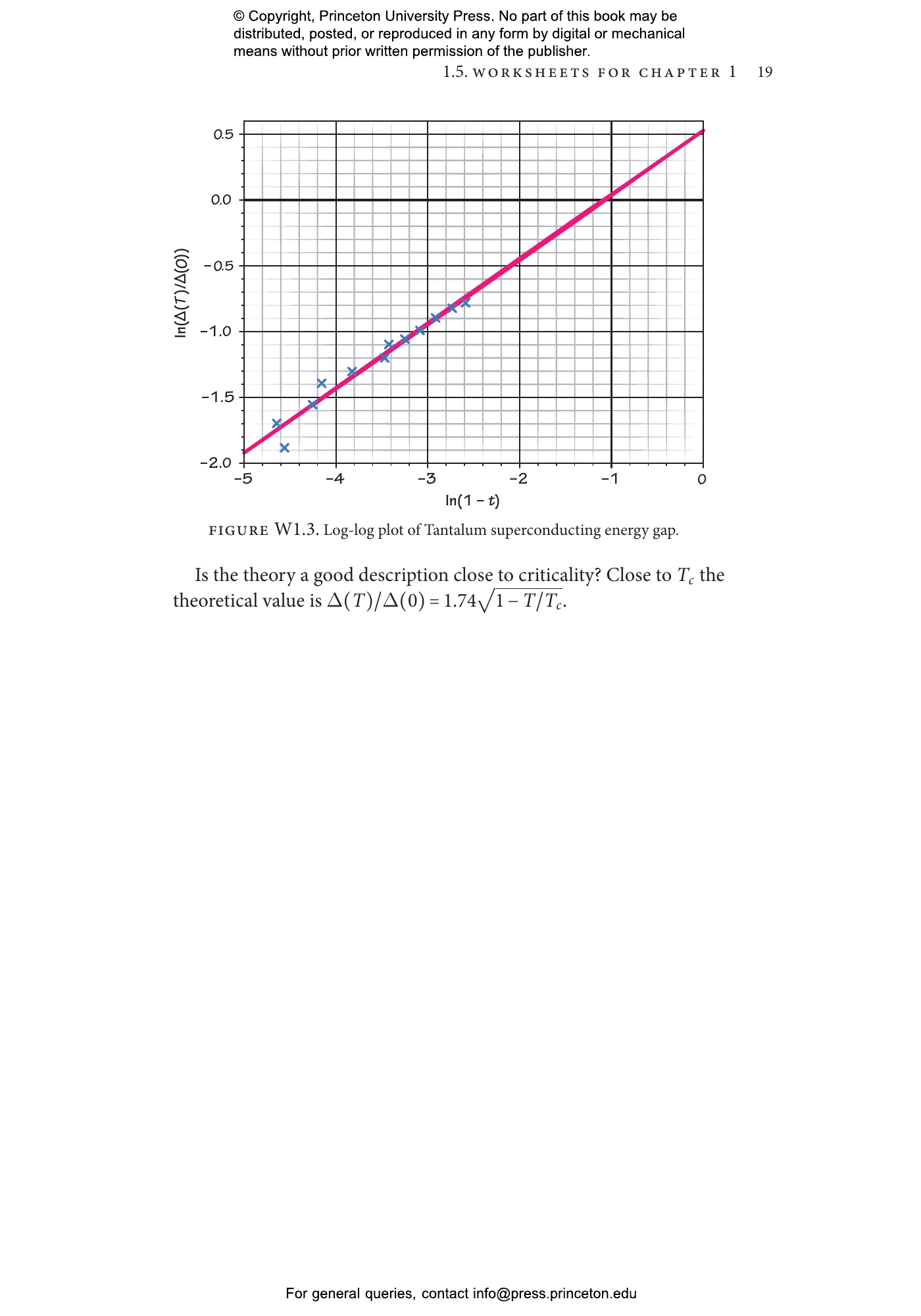
Statistical mechanics deploys a powerful set of mathematical approaches for studying the thermodynamic properties of complex physical systems. This textbook introduces students to the statistical mechanics of systems undergoing changes of state, focusing on the basic principles for classifying distinct thermodynamic phases and the critical phenomena associated with transitions between them. Uniquely designed to promote active learning, Statistical Mechanics of Phases and Phase Transitions presents some of the most beautiful and profound concepts in physics, enabling students to obtain an essential understanding of a computationally challenging subject without getting lost in the details.
- Provides a self-contained, conceptually deep introduction to the statistical mechanics of phases and phase transitions from a modern perspective
- Carefully leads students from spontaneously broken symmetries to the universality of phase transitions and the renormalization group
- Encourages student-centric active learning suitable for both the classroom and self-study
- Features a wealth of guided worksheets with full solutions throughout the book that help students learn by doing
- Includes informative appendixes that cover key mathematical concepts and methods
- Ideal for undergraduate physics majors and beginning graduate students
- Solutions manual for all end-of-chapter problems (available only to instructors)
Steven A. Kivelson is the Prabhu Goel Family Professor of Physics at Stanford University. Jack Mingde Jiang received a PhD in applied physics from Stanford. Jeffrey Chang is a PhD student in the Department of Physics at Harvard University.
- Preface
- A Notational Note
- Acknowledgements
- 1 Overview
- 1.1 Phases
- 1.1.1 Phase Diagrams
- 1.1.2 Phase Transitions
- 1.1.3 The Critical Point
- 1.1.4 Continuous and Discontinuous Transitions
- 1.1.5 Distinction between Phases
- 1.2 Symmetries
- 1.2.1 The Cubic-to-Tetragonal Transition
- 1.2.2 Solids, Liquids, and Gases
- 1.2.3 Ferromagnets
- 1.3 Universality
- 1.3.1 Critical Exponents
- 1.3.2 Universality Classes
- 1.4 Problems
- 1.5 Worksheets for Chapter 1
- 2 Background: Fundamentals of Statistical Mechanics
- 2.1 Review of Statistical Mechanics
- 2.1.1 The Link between Thermodynamics and Statistical Mechanics
- 2.1.2 The Thermodynamic Limit
- 2.1.3 Derivatives of the Free Energy
- 2.1.4 Variance and Fluctuations
- 2.1.5 Covariance and Correlation Functions
- 2.1.6 Correlation Functions and Phases of Matter
- 2.2 *Other Fundamental Issues Concerning Statistical Mechanics
- 2.3 Symmetry
- 2.3.1 Meaning of “Symmetry”
- 2.3.2 Symmetries in Statistical Mechanics
- 2.4 Problems
- 2.5 Worksheets for Chapter 2
- W2.1 Calculating Thermal Averages
- W2.2 Identifying Symmetries
- 3 The Ising Model
- 3.1 Definition
- 3.1.1 What We Would Like to Know
- 3.2 Qualitative Properties
- 3.2.1 The Droplet Argument in d= 2
- 3.2.2 Low-TSeries Expansion in Arbitrary d
- 3.3 Solution in Zero Dimensions
- 3.3.1 J= 0 Limit in dDimensions
- 3.4 Solution in One Dimension
- 3.4.1 h= 0 Solution—The Combinatorics Approach
- 3.4.2 The General Solution Using the Transfer Matrix Approach
- 3.5 Solution in Two Dimensions
- 3.6 Variations on the Ising Model
- 3.7 *Low TExpansion, High TExpansion, and Duality
- 3.7.1 Low-Temperature Expansion to All Orders
- 3.7.2 High-TSeries Expansion in Arbitrary d
- 3.7.3 Duality
- 3.8 Problems
- 3.9 Worksheets for Chapter 3
- W3.1 The Ising Hamiltonian—A Primer
- W3.2 More on the 4-Site Problem
- W3.3 The Droplet Argument in 2D
- W3.4 Low-Temperature Expansion in 2D
- W3.5 Ising Model in 0D
- W3.6 Ising Model in 1D—The Combinatorics Approach
- W3.7 Ising Model in 1D—The Transfer Matrix Approach
- 4 Mean-Field Theory
- 4.1 Intuitive Introduction
- 4.2 The Variational Principle
- 4.2.1 Usefulness of the Variational Approach
- 4.2.2 An Illustration of the Principle
- 4.3 Mean-Field Theory of the Ising Model
- 4.3.1 The Mean-Field Phase Diagram
- 4.4 Variational Free Energy as Function of mj
- 4.4.1 Expansion for Small m
- 4.4.2 Critical Exponents
- 4.4.3 *Metastability and Two-Phase Coexistence
- 4.5 Validity of Mean-Field Theory
- 4.6 Problems
- 4.7 Worksheets for Chapter 4
- W4.1 Weiss Mean-Field Theory
- W4.2 Variational Principle
- W4.3 *Variational Mean-Field Theory—General Features
- W4.4 Mean-Field Solution of the Ising Model
- W4.5 Low Temperature Analysis of Mean-Field Equations
- W4.6 The Variational Free Energy Fvar as a Function of the Order Parameter
- W4.7 The Mean-Field Critical Exponents β,γ,δ
- 5 Broken Symmetries
- 5.1 Spontaneously Broken Symmetry and Order Parameters
- 5.1.1 Why the Thermodynamic Limit Is Necessary
- 5.1.2 Phase Transitions in the Real World
- 5.2 Examples of Broken Symmetries
- 5.2.1 Order-Disorder Transitions
- 5.2.2 Structural Transitions
- 5.2.3 Crystalline Solids
- 5.2.4 Liquid Crystals
- 5.2.5 Ferromagnetism
- 5.2.6 Superfluids
- 5.2.7 Superconductors
- 5.3 Order Parameters and Symmetry
- 5.3.1 Thermodynamic Role of the Order Parameter
- 5.4 Some Paradigmatic Models
- 5.4.1 Models with Discrete Symmetries
- 5.4.2 Models with Continuous Symmetries
- 5.5 Problems
- 5.6 Worksheets for Chapter 5
- W5.1 Liquid Crystals and Broken Symmetries
- W5.2 Interpolating between the XY and Clock Models
- W5.3 Determining the Symmetry and Order Parameter
- 6 The Landau Free Energy
- 6.1 Once More, the Ising Model
- 6.2 Other Symmetries
- 6.2.1 The XY Model: O(2) Symmetry
- 6.2.2 q-State Clock Models
- 6.3 Multicritical Points
- 6.3.1 Tricritical Points
- 6.3.2 Bicritical and Tetracritical Points
- 6.4 Problems
- 6.5 Worksheets for Chapter 6
- W6.1 Deducing the Landau Free Energy from Symmetry Considerations
- W6.2 Understanding the Discontinuous Transition with a ϕ3 Term
- 7 Ginzburg-Landau Theory
- 7.1 The Thermodynamic Correlation Length
- 7.2 Spatial Correlations in the Ising Model
- 7.2.1 Position-Dependent Correlation Functions
- 7.2.2 Calculating the Nonlocal Susceptibility χij
- 7.3 The Effective Field Theory
- 7.3.1 Taking the Continuum Limit
- 7.3.2 The Equilibrium Order Parameter Field
- 7.3.3 Correlations in the Ordered Phase
- 7.4 Beyond the Ising Model
- 7.5 Order Parameter Textures
- 7.5.1 Domain Walls in the Ising Ferromagnet
- 7.5.2 Textures in the XY Model
- 7.5.3 Vortices in the XY Model
- 7.6 Equilibrium Fluctuations
- 7.7 Problems
- 7.8 Worksheets for Chapter 7
- W7.1 The Meaning of the Correlation Length
- W7.2 Ising Model with Spatial Variation
- W7.3 Estimating a Correlation Length from the Lattice Correlation Function
- W7.4 Deriving the Ginzburg-Landau Functional from Symmetry Arguments
- W7.5 Solving for the Continuum Correlation Length
- W7.6 Susceptibility of the XY Model for T < Tc
- W7.7 A Domain Wall in an Ising System
- 8 *The Self-Consistent Gaussian Approximation
- 8.1 The Gaussian Model
- 8.1.1 The Nature of the Solution
- 8.1.2 Higher Order Correlations and Wick’s Theorem
- 8.2 Using the Gaussian Model in a Variational Approximation
- 8.2.1 The Symmetric Phase at T > Tc
- 8.3 ∗Exact Results for O(N) Model as N→∞
- 8.3.1 The Ordered Phase and the Mermin-Wagner Theorem
- 8.4 Worksheets for Chapter 8
- W8.1 Gaussian Integrals and Wick’s Theorem (Isserlis’s Theorem)
- W8.2 Mean-Field Approximations to the 0D ϕ4 Theory
- 9 *Quenched Disorder
- 9.1 Systems with Quenched Disorder
- 9.2 Configuration Averages
- 9.2.1 Example: Array of Harmonic Oscillators
- 9.3 Gaussian Model in a Random Field
- 9.4 The Imry-Ma Argument
- 9.5 Larkin-Ovchinikov-Lee-Rice Argument
- 9.6 Other Effects of Disorder
- 10 *Renormalization Group Perspective
- 10.1 Scaling Theory
- 10.1.1 Relevant and Irrelevant Perturbations
- 10.2 Renormalization Group—Overview
- 10.2.1 The Nature of the RG Transformation
- 10.3 RG for the Central Limit Theorem
- 10.4 The RG in Slightly Less than 4D
- 10.5 Beyond Broken Symmetry: Superconductors, Topological Order, Gauge Theories
- 10.6 Problems
- 10.7 Worksheets for Chapter 10
- W10.1 Renormalization Group of the 1D Ising Chain
- W10.2 Perturbative Renormalization Group of the ϕ4 Theory in dDimensions
- A Appendices
- A.1 The Qubit and Pauli Matrices
- A.2 Low-Temperature Expansion of the Ising Model
- A.3 The Fourier Series and Transforms
- A.4 The Calculus of Variations
- A.5 The Continuum Limit
- A.6 Fourier Transform of a Lorentzian: The Ornstein-Zernike Law
- A.6.1d= 1
- A.6.2 d= 3
- A.6.3 Arbitrary d
- A.6.4 At Criticality: Orenstein-Zernike as κ→ 0.
- A.7 Review of Probability
- A.8 Deriving the Variational Principle for Noncommuting Hamiltonians
- A.9 Properties of Gaussian Distributions and Wick’s Theorem
- A.10 Rudiments of Group Theory
- A.10.1 Symmetries as a Group: An Example in a Triangle
- A.11 Validity of Mean-Field Theory in an Ising Ferromagnet with Long-Range Interactions
- A.12 More about the Broken Symmetry in Superfluids
- B Worksheet Solutions
- B.1 Chapter 1 Worksheet Solutions
- B.2 Chapter 2 Worksheet Solutions
- B.2.1 Calculating Thermal Averages
- B.2.2 Identifying Symmetries
- B.3 Chapter 3 Worksheet Solutions
- B.3.1 The Ising Hamiltonian—A Primer
- B.3.2 More on the 4-Site Problem
- B.3.3 The Droplet Argument in 2D
- B.3.4 Low-Temperature Expansion in 2D
- B.3.5 Ising Model in 0D
- B.3.6 Ising Model in 1D—The Combinatorics Approach
- B.3.7 Ising Model in 1D—The Transfer Matrix Approach
- B.4 Chapter 4 Worksheet Solutions
- B.4.1 Weiss Mean-Field Theory
- B.4.2 Variational Principle
- B.4.3 *Variational Mean-Field Theory—General Features
- B.4.4 Mean-Field Solution of the Ising Model
- B.4.5 Low Temperature Analysis of Mean-Field Equations
- B.4.6 The Variational Free Energy Fvar as a Function of the Order Parameter
- B.4.7 The Mean-Field Critical Exponents β,γ,δ
- B.5 Chapter 5 Worksheet Solutions
- B.5.1 Liquid Crystals and Broken Symmetries
- B.5.2 Interpolating between the XY and Clock Models
- B.5.3 Determining the Symmetry and Order Parameter
- B.6 Chapter 6 Worksheet Solutions
- B.6.1 Deducing the Landau Free Energy from Symmetry Considerations
- B.6.2 Understanding the Discontinuous Transition with a ϕ3 Term
- B.7 Chapter 7 Worksheet Solutions
- B.7.1 The Meaning of the Correlation Length
- B.7.2 Ising Model with Spatial Variation
- B.7.3 Estimating a Correlation Length from the Lattice Correlation Function
- B.7.4 Deriving the Ginzburg-Landau Functional from Symmetry Arguments
- B.7.5 Solving for the Continuum Correlation Length
- B.7.6 Susceptibility of the XY Model for T < Tc
- B.7.7 A Domain Wall in an Ising System
- B.8 Chapter 8 Worksheet Solutions
- B.8.1 Gaussian Integrals and Wick’s Theorem (Isserlis’s Theorem)
- B.8.2 Mean-Field Approximations to the 0D ϕ4 Theory
- B.10 Chapter 10 Worksheet Solutions
- B.10.1 Renormalization Group of the 1D Ising Chain
- B.10.2 Perturbative Renormalization Group of the ϕ4 Theory in dDimensions
“With its unique and strong emphasis on worksheets, this is a very useful addition to the large pedagogical literature on phase transitions. Kivelson, Jiang, and Chang have provided a comprehensive account of phase transitions at a level that will be instructive for advanced undergraduates and graduate students in physics, and suitable for most standard courses on this topic.”—Nigel Goldenfeld, University of California, San Diego
“Phase transitions are weird. Usually in physics, things happen in a smooth, continuous fashion. But, at a phase transition, the slightest nudge causes a system to change dramatically and discontinuously, as water cracks and freezes, or bubbles and boils. Kivelson, Jiang, and Chang do a great job of taking the reader gently by the hand and leading them through the subtle and beautiful story of phases and how they change.”—David Tong, University of Cambridge
“With a focus on the statistical mechanics of continuous phase transitions, this textbook presents many of the key calculations in the field in thoughtful detail while introducing many useful concepts and methods of broad importance.”—James Sethna, Cornell University
“Statistical Mechanics of Phases and Phase Transitions uses comparatively easy language to communicate essential ideas and techniques, drawing on a high level of scholarship and covering many important and interesting concepts.”—Jin Yu, University of California, Irvine
“Statistical Mechanics of Phases and Phase Transitions is not a list of facts or applications but a story told in an engaging and sympathetic way. It is also remarkably extensive in the material it covers, from the basics to graduate level. This marvelous book makes a hard subject accessible.”—Ralph Kenna, Coventry University